Topological Data Analysis – PersLay: Neural Layers for Persistence Diagrams
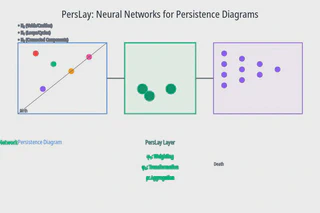 PersLay: Neural network layer for processing persistence diagrams and encoding topological features into deep learning architectures.
PersLay: Neural network layer for processing persistence diagrams and encoding topological features into deep learning architectures.This project was conducted as part of the Topological Data Analysis for Imaging and Machine Learning course at ENS Paris-Saclay (Master MVA).
The objective was to study and reproduce PersLay (Carrière, Chazal, Ike, Lacombe, Royer, & Umeda, 2020), a neural network layer designed to vectorize persistence diagrams and integrate topological information directly into deep learning architectures.
Background
Persistence diagrams are key representations in topological data analysis (TDA), capturing the evolution of homological features across scales.
However, their irregular structure makes them difficult to incorporate in traditional machine learning models.
Previous approaches relied on:
- Kernel-based vectorizations (e.g. persistence images)
- Handcrafted embeddings (e.g. Deep Sets, landscape functions)
- Fixed signatures with limited task adaptability
PersLay addresses these limitations by learning the vectorization end-to-end, adapting its representation to the target task.
Implementation and Study
We analyzed the PersLay architecture, which combines:
- A learnable point transformation function (Gaussian, triangular, or linear)
- A weighting function ensuring permutation invariance
- A summation operator (op = sum) aggregating transformed diagram points
The network was trained on graph classification tasks (MUTAG, ORBIT5K, ORBIT100K) using:
- Extended persistence diagrams to capture both sublevel and superlevel filtrations
- Heat kernel signatures from graph Laplacians as additional features
Experiments and Findings
Our experiments replicated key results from the original paper:
- ORBIT5K dataset: matched or exceeded state-of-the-art kernel-based methods.
- ORBIT100K dataset: PersLay scaled efficiently, where classical kernel methods failed.
- Ablation studies: grid size had limited influence on accuracy, but overly large grids led to overfitting.
- Permutation operators: simple sum aggregation achieved the best stability and generalization.
We further investigated the effect of the diffusion parameter \(t\) in heat kernel signatures, showing that classification performance remained stable across a wide range of values.
Key Insights
- Adding graph topology substantially improved classification accuracy.
- Extended diagrams were essential to capture loop geometries and higher-order structures.
- PersLay provided a trainable, efficient vectorization with reduced computational cost compared to kernel methods.
- The framework can be extended to image or manifold data, beyond graph-based applications.
References
- Carrière, M., Chazal, F., Ike, Y., Lacombe, T., Royer, M., & Umeda, Y. (2020). PersLay: A Neural Network Layer for Persistence Diagrams and New Graph Topological Signatures.
- Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R., & Smola, A. (2017). Deep Sets.
- Sun, J., Ovsjanikov, M., & Guibas, L. (2009). A concise and provably informative multi-scale signature based on heat diffusion.